Зміст
Вільне падіння – падіння тіл у безповітряному просторі під дією сили тяжіння. Є рівноприскореним рухом.
Падіння тіл у повітрі можна приблизно вважати вільним лише за умови, що опір повітря мало і його можна знехтувати.

У разі вільного падіння всі тіла, незалежно від їхньої маси, падають з однаковим прискоренням, яке називають прискоренням вільного падіння ( g ). Вектор прискорення вільного падіння завжди спрямований вертикально донизу.
Прискорення вільного падіння – це прискорення, яке набувають усі тіла при вільному падінні поблизу поверхні незалежно від їхньої маси.
У поверхні Землі прискорення вільного падіння вважається постійною величиною і розраховується за формулою:
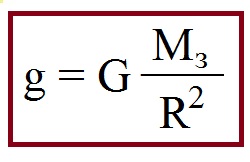
G = 6,67408(31)·10 −11 Н·м²·кг −2 – гравітаційна стала;
M – маса Землі;
R – радіус Землі.
У цьому значення прискорення вільного падіння приблизно дорівнює
g = 9,81 м/с².
Прискорення вільного падіння залежить від відстані між центром планети та піднятим над її поверхнею тілом.
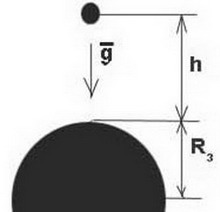
Для більш точного розрахунку застосовують формулу:
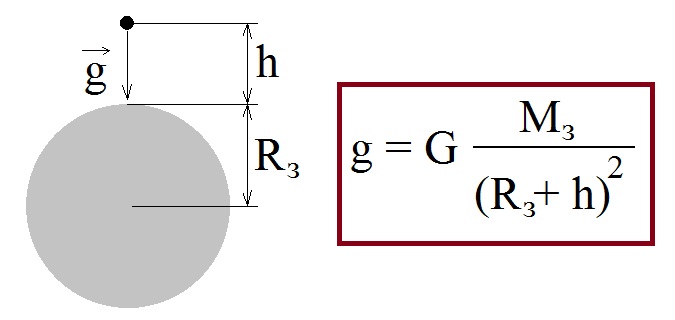
h-висота підйому тіла над поверхнею Землі;
Rз – радіус Землі
Прискорення вільного падіння залежить від маси падаючого тіла! Вектор прискорення вільного падіння завжди спрямований до центру Землі.
Прискорення вільного падіння залежить:
1. від географічної широти;
оскільки Земля сплюснута біля полюсів через обертання навколо своєї осі
на полюсі g = 9,832 м/с²
на екваторі = 9,78 м/с²
Точні значення прискорення вільного падіння для падаючих тіл на полюсі та на екваторі будуть різні через неправильну форму Землі.
2. від висоти підйому тіла над поверхнею Землі;
поблизу Землі прискорення вільного падіння вважається рівним
9,8 м/с²
3. від гравітаційних аномалій Землі, тобто. поклади з корисними копалинами спотворюють значення прискорення вільного падіння у цих областях.
Для інших планет прискорення вільного падіння визначається аналогічно. На кожній планеті прискорення вільного падіння залежить від радіусу та маси даної планети:
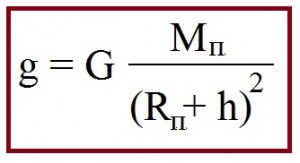
Формула прискорення вільного падіння
Прискорення вільного падіння – прискорення, що повідомляється вільній матеріальній точці силою тяжіння, піднятою на невелику відстань над Землею.
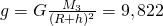
Якщо застосувати цю формулу для обчислення гравітаційного прискорення на Землі, ми отримаємо:
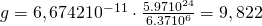
У разі Землі падіння тіл вважається умовно вільним, т.к. при падінні тіла у повітряному середовищі завжди виникає ще й сила опору повітря.
Ідеальне вільне падіння можливе лише у вакуумі, де немає сили опору повітря, і незалежно від маси, щільності та форми всі тіла падають однаково швидко, тобто у будь-який момент часу тіла мають однакові миттєві швидкості та прискорення.
Спостерігати ідеальне вільне падіння тіл можна в трубці Ньютона, якщо за допомогою насоса викачати повітря.

Поблизу поверхні Землі величина сили тяжіння вважається постійною, тому вільне падіння тіла – рух тіла під дією постійної сили. Отже, вільне падіння – це рівноприскорений рух.
Експериментально встановлено, що прискорення вільного падіння не залежить від маси падаючого тіла, але залежить від географічної широти місцевості q і висоти h підйому над земною поверхнею. При цьому залежність g від q подвійна.
По-перше, Земля — не куля, а еліпсоїд обертання, тобто радіус Землі на полюсі менший за радіус Землі на екваторі. Тому сила тяжкості і прискорення вільного падіння , що викликається нею , на полюсі більше, ніж на екваторі (g=9,832 на полюсі і g = 9,780 на екваторі).
По-друге, Земля обертається навколо своєї осі і це впливає на прискорення вільного падіння , що призводить до його залежності від географічної широти місцевості.
У формулі ми використовували:
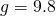
Прискорення вільного падіння на Землі
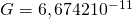
Гравітаційна постійна
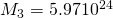
Маса Землі
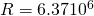
Радіус Землі
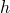
Висота тіла над поверхнею Землі
Прискорення вільного падіння на Марсі
Прискорення вільного падіння лежить на поверхні Марса в 2,65 разів менше прискорення вільного падіння лежить на Землі. Радіус Марса приблизно дорівнює 3400 км. У скільки разів маса Марса менша за масу Землі?
Із закону всесвітнього тяжіння випливає, що значення гравітаційного прискорення g на поверхні планети пов’язане з масою планети M таким співвідношенням:
g= GMR2 (1)
де G, M, R – відповідно гравітаційна стала, маса планети, радіус планети.
З (1) виразимо масу: M=gR2G (2)
Запишемо формулу для маси Землі з індексом 1, а для маси Марса – з індексом 2:
M1=g1R21G (3)
M2=g2R22G (4)
Шукане ставлення:
n =M1M2=g1R21Gg2R22G (5)
Згідно з умовою g1g2= 2 , 65, Тоді вираз (5) набуває вигляду (6):
n = 2 , 65 ∗R21R22 (6)
n = 2 , 65 ∗6371000234000002≈ 9 , 3
Відповідь: маса Марса в 9,3 рази менша від маси Землі



















