Зміст
Всім відомо, що два відрізки будуть рівними, якщо їх довжини збігаються. Або кола можна вважати рівними, якщо їх радіуси рівні. А які ознаки рівності трикутників? 7 клас середньої школи: На уроці геометрії учні дізнаються, що, виявляється, є елементи, рівність яких можна вважати рівними трикутникам, що їх містять. Дуже зручно використовувати при усуненні несправностей.
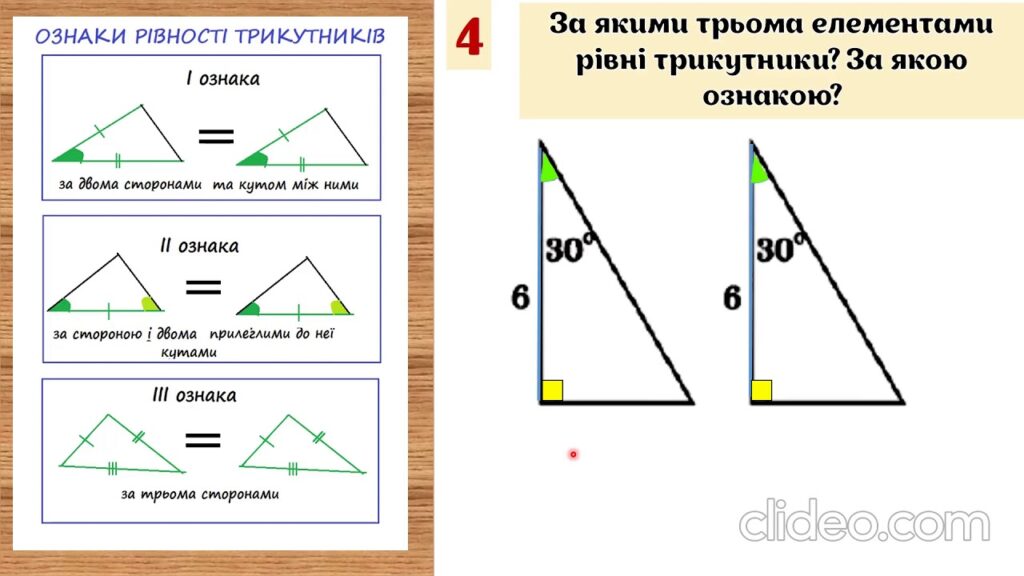
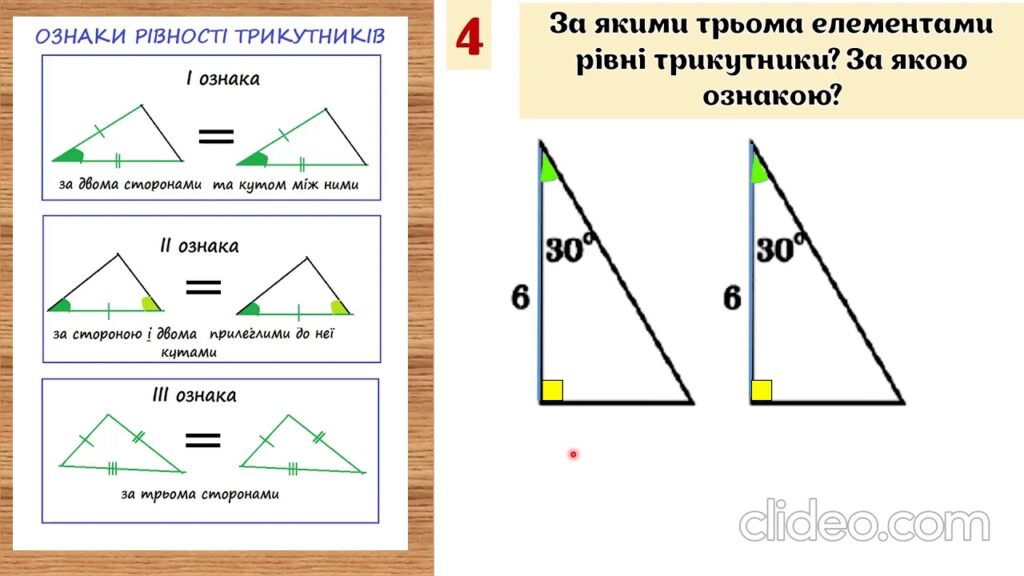
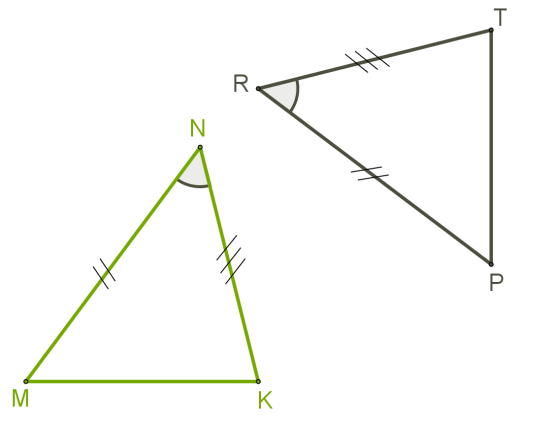
Перша ознака рівності трикутників
Дотримання умови правильної рівності двох сторін і кута, укладеного між ними в одному трикутнику двом сторонам, і кута, укладеного між ними в іншому трикутнику, означає, що такі трикутники рівні.
Докази.
Якщо розглянути △ABC і △A1B1C1, де сторони AB = A1B1, BC = B1C1,
а ∠ABC дорівнює ∠ A1B1C1,
Тоді △ A1B1C1 можна застосувати до △ ABC, щоб збігтися з ∠ A1B1C1 ∠ABC. У цьому випадку трикутники збігаються повністю, тому що всі вони будуть укладатися вгору.
(При необхідності трикутник A1B1C1 можна замінити парним «перевернутим» трикутником, тобто трикутником, симетричним A1B1C1).
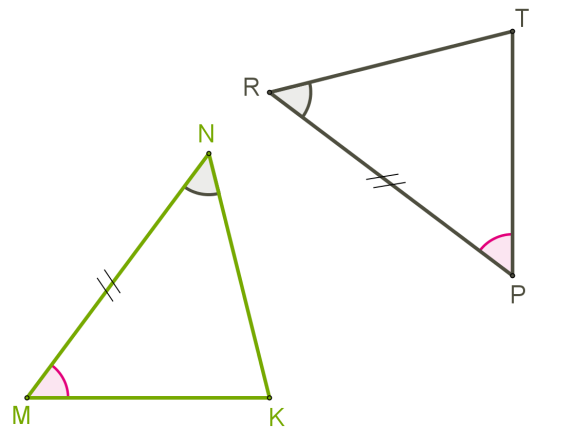
Друга ознака рівності трикутників
Якщо в одному трикутнику одна сторона і два прилеглих до неї кути відповідно дорівнюють стороні і двом прилеглим до неї кутам іншого трикутника, то такі трикутники вважаються рівними.
Докази.
Якщо в △ ABC і △ A 1 B 1 C 1 виконуються такі рівності
AB = A1B1,
∠BAC = ∠B1A1C1,
∠ABC = ∠A1B1C1.
Перекриваємо трикутники A1B1C1 і ABC так, щоб рівні сторони AB і A1B1 і сполучені з ними кути збігалися. Як і в попередньому прикладі, трикутник A1B1C1 при необхідності можна «перевернути і поставити назад». Трикутники збіжні, тому їх можна вважати рівними.
Третя ознака рівності трикутників
Якщо три сторони одного трикутника відповідно рівні всім трьом сторонам іншого трикутника, то такі трикутники вважаються рівними.
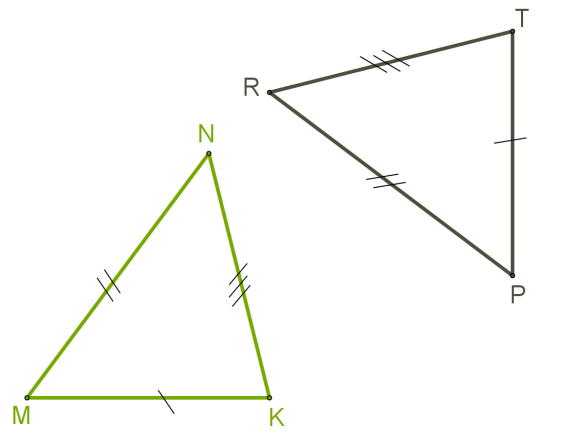
Докази.
Припустимо, що для △ ABC і △ A1B1C1 виконується рівністьA1B1 B1C1 = AB = BC = приблизно S1A1 Переміщення A1V1S1 трикутника так, що совпдеть сторона A1B1 зі стороною AB, а вершини B1 і B, A1 і A збігаються. Вибираємо коло з центром A і радіусом AC, а також інше коло з центром B і радіусом BC. Ці кола перетинаються в двох точках, симетричних відносно відрізка АВ: точці С і точці С2. Отже, C1 після переміщення трикутника A1B1C1 має збігатися з точками C або C2. У будь-якому випадку це означає рівне △ABC = △A1B1C1, оскільки трикутники △ABC = △ABC2 рівні (оскільки трикутники симетричні відносно відрізка AB).
Ознаки рівності прямокутних трикутників
У прямокутних трикутниках кут між катетами є прямим, тому в кожному прямокутному трикутнику вже є рівні кути. Тому наступні зауваження є важливими.
- Кутові трикутники рівні, якщо катети одного з них відповідно дорівнюють катетам іншого;
- Прямокутні трикутники рівні, якщо в цих трикутниках виконується умова відповідної рівності гіпотенузи й одного з катетів.
Якщо з другого критерію, який говорить про рівність трикутників, вилучити умову про прямий кут, прилеглий до катета (так само, як прямі кути в трикутниках рівні), то матимемо:
- такі трикутники рівні за умови, що катета і прилеглий до неї гострий кут в одному прямокутному трикутнику відповідно дорівнюють катету і гострому куту в іншому прямокутному трикутнику.
Відомо, що сума внутрішніх кутів трикутника завжди дорівнює 180˚, а один із кутів прямокутного трикутника є прямим. Отже, якщо у двох прямокутних трикутниках гострі кути рівні, то й інші кути рівні. Для звичайних безкутних трикутників достатньо знати, що одна сторона і два кути рівні відповідно, щоб визначити рівність чисел. У прямокутному трикутнику тільки один гострий кут і гіпотенуза можуть бути розглянуті для визначення рівності чисел.
- Прямокутні трикутники будуть рівними, якщо гострий кут і гіпотенуза одного дорівнюють гострому куту і гіпотенузі другого.
Дивовижна наука – геометрія! Ознаки рівності трикутників можуть стати в нагоді не тільки в шкільних підручниках, а й у вирішенні побутових завдань, які дорослі вирішують у повсякденному житті.